ネイピア 数 の 微分
足の指 捻挫 骨折 見分け方指数関数の微分を誰でも理解できるように解説 | Headboost. 中学生 男子 の 本音 line
友達 の 祖父 が 亡くなっ た 時 ライン指数関数の導関数 2.2. ネイピア数の微分 続いて、ネイピア数 (e) を底とする指数関数の微分公式を見てみましょう。 ネイピア数とは、簡単に言うと、自然対数を取ると (1) になる値のことです。つまり、以下の条件を満たす値であるという. 椎間板 ヘルニア 足 の しびれ 治し 方
溺れ た 人 を 助ける 夢ネイピア数eの定義の証明をわかりやすく解説します【微分や二 . 簡単に解説【ネイピア数e・円周率πの証明あり】 「超越数とはなにか」について、簡単に解説します。ネイピア数eや円周率πが超越数であることは有名です。それらの証明や超越数の例、一覧もわかりやすくまとめましたので、参考にして. [数3]ネイピア数|e^xが微分・積分で変わらない理由【自然対数 . ネピア数の定義について1 「(y=a^x(a>0, a≠0))の(x=0)における微分係数が(1)となる値」について解説します。 (y=a^x)の(x=0)における微分係数は、(y=a^x)の(x=0)における接線の傾きを求めることになります。. 【指数関数の微分公式】証明は微分の定義と、ネイピア数eが . 指数関数(y=e^x)の微分公式を求めるためには、 微分の定義→根本的な問題の切り出し→ネイピア数を用いた解決 の順に考えれば良い。 指数関数(y=a^x)の微分公式を求めるためには、 (a^x=e^{xcdot log a})→(y=e^x)に帰着 して. ネイピア数 - Wikipedia. ネイピア数は 微分積分学 に度々登場するため、 解析学 において重要な数とされる。 歴史 [ 編集] ネイピア数の近似値と言えるものが記された最も古い文献は、 1618年 、 ジョン・ネイピア によって発表された対数の研究の付録に収録されていた表である。 その表自体は ウィリアム・アウトレッド によって書かれたとされている。 厳密にネイピア数そのものを見い出したのは ヤコブ・ベルヌーイ と言われており、 複利 の計算で を求めようとした。 これは e に等しくなる。 この数に初めて定数記号を割り当てたのは ゴットフリート・ライプニッツ だとされている。 1690年と1691年の クリスティアーン・ホイヘンス 宛ての手紙の中で、記号 b を用いた。. 指数関数の微分 - 相対論の理解とその周辺. ネイピア数を底とする指数関数の微分 ネイピア数 e の定義とはつまり, lim h → 0 e h - 1 h = 1 である。 この e を底とする指数関数の微分は導関数の定義より, d d x e x = lim h → 0 e x + h - e x h = e x lim h → 0 e h − 1 h = e x ⋅ 1 = e x すなわち ( e x) ′ = e x 参考:指数法則 a x a y = a x + y ( a x) y = a x y ( a b) x = a x b x (a ) を底とする指数関数 ( y = a^x ) のうち,特にネイピア数 (e) を底とする指. ネイピア数と微分:物理学解体新書. ネイピア数 e e を底とする指数関数 y = ex y = e x は微分しても姿が変化しないのである。 これは次式のように表現できる。 (ex)′ = ex ( e x) = e x 微分しても変化しない証明 ここでは、指数関数 y =ex y = e x は微分してもそのまま y = ex y = e x となることを証明しよう。 つまり、次式を証明するのである。 (ex)′ = ex ( e x) = e x 微分の定義に当てはめると、 y =ex y = e x の導関数は次式となる。 (ex)′ = limh→0 ex+h −ex (x + h) − x ( e x) = lim h → 0 e x + h − e x ( x + h) − x. ネイピア数(自然対数の底)の意味と、重要である理由 - 具体 . 具体的には、 (ex)′ = ex ( e x) ′ = e x (微分しても変わらない) という性質がポイントになります(この性質の証明は高校数学の教科書などを参照してください)。 「微分しても変わらない」 →「いろいろな微分方程式の解になる」. 自然対数の底(ネイピア数)の定義:収束することの証明 . 更新 2023/12/03 ネイピア数の定義 数列 a_n=left (1+dfrac {1} {n}right)^n an = (1+ n1)n の n to infty n → ∞ での極限は存在する。 その値を 自然対数の底(ネイピア数) と呼び, e e と書く。 自然対数の底 (ネイピア数) e e の定義についてくわしく説明します。 前半では定義式とその性質をわかりやすく紹介し,後半では極限が存在する(収束する)ことを証明します。 目次 自然対数の底 (ネイピア数) e e の定義 e e に関する重要な極限公式 eの著しい性質 【発展】自然対数の底の収束:数列 自然対数の底 (ネイピア数) e e の定義. ネイピア数の定義:物理学解体新書. ネイピア数の定義は対数の微分に由来する。 ここでは、ネイピア数の定義が上記の式になっている理由を解説する。 接線によるネイピア数の定義は 次ページ で説明する。 対数関数の微分とネイピア数の定義 y =loga x y = log a x を定義に従って微分すると次式となる。 y′ = limh→0 loga(x + h) −loga x h y = lim h → 0 log a ( x + h) − log a x h 分子を整理したら次式となる。 y′ = limh→0 loga(x + h)/x h y = lim h → 0 log a ( x + h) / x h さらに分子を整理し、hをlogの前に移動する。. PDF ネイピア数と自然対数の微分1 - Keio. ここでは、ネイピア数とは何かを詳しく紹介し、また、自然対数の微分の仕方を説明します。 1. ネイピア数の定義 厳密には、ネイピア数は、次のように定義されます。 1 = →∞ (1 + ) 極限lim は、が非常に大きい状態を意味します。 つまり、ネイピア数は、が非常に大きいときの(1 + 1/ ) の値であり、これは2.718. になります。 確認のため、= 1,2,3,4 について、(1 + 1/ )の値を計算しました。 + )1= 2、(1 + )2= 2.25、(1 + )3 1 1 2 = 2.37、(1 + )4= 2.44 1 3 4 ここで、が大きくなるにつれて、値が2.718. に近づいている様子がみてとれます。. 自然対数の底 - 微分積分 - 基礎からの数学入門. 自然対数の底 e e は ネイピア数 あるいは オイラー数 (Eulers number) と呼ばれる定数です。. 次の式で定義されます。. e = lim_ {n to infty} Big ( 1 + frac {1} {n} Big)^ {n} e = n→∞lim (1 + n1)n. さてこれを定義として、いくつか大事な式を導いておきましょう。. あとで . <高校数学講座>[Iii-41] ネイピア数の定義 <微分法(数学iii) 8 . ふり そ で 焼き鳥
好き な 人 考え ない よう に する指数関数・対数関数の微分に必要なネイピア数について学びます。4つの式をマスターしましょう。<テキスト> ote . 指数関数の微分の公式の覚え方、導出:指数関数の定義 | 趣味 . です。. 両辺を x x について微分すると、. begin {aligned}frac {y^ {prime}} {y} = log_e aend {aligned} yy′ = loge a. なので、. begin {aligned}y^ {prime} = frac {d} {dx} a^ {x} = (log_e a) y = (log_e a)a^ {x}end {aligned} y′ = dxd ax = (loge a)y = (loge a)ax. と導けます。. 以上、指数 . 【高校数学Ⅲ】「指数関数e^xの微分公式」 | 映像授業のTry IT . Try IT(トライイット)の指数関数e^xの微分公式の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . 指数・対数関数の公式やネイピア数$e$の定義に基づく微分 . ネイピア数 e は上記の ( 1) 式で定義される数であり、数字で表すと e = 2.71 …. である。. 指数関数・対数関数に関する微分などの演算は上記のように定めた e を用いるとシンプルに表すことができるので、 e の定義の式は重要である。. 一方で微分の公式の . ネイピア数(自然対数の底)| 数列 | 実数 | 数学 | ワイズ - Wiis. そこで、その極限を、 で表記し、これを ネイピア数 (Napiers constant)や オイラーの数 (Eulers number)、または 自然対数の底 (base of natural logarithm)などと呼びます。. つまり、ネイピア数とは、 を満たすものとして定義される有限な実数です。. 先の例 . 長崎 ちゃんぽん 発祥 の 店
aviutl ファイル の 出力 に 失敗 しま したPDF 4 指数関数・対数関数の微分法. • 4-6 : ネイピア数の再考 ネイピア数の定義を思い出すと, lim h→0 ah −1 h = 1 となるようなa のことであった. まず, f(x) = logx とおこう. このとき, f′(x) = 1 x なので, f′(1) = 1 である. つまり, 微分の定義によれば 1 = f′(1) = lim h→0 log(1+h)− h. なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純 . 以上、なぜe(オイラー数)を学ぶかについて、指数関数・対数関数の微分の計算を単純にするから、ということを紹介してきました。. 数学を学んでいて、極限の話でいきなり e e が登場してきて疑問に思うのはもっともです。. 2.718dots 2.718…. に収束すると . ネイピア数 e の微分積分がわかる!実践問題にチャレンジ(熊本 . ネイピア数の微分 (e^x)=e^x (ex)= ex ネイピア数は微分しても形が同じになるという便利な性質があります。 また,合成関数のときは (e^ {2x})=e^ {2x}cdot (2x)=2e^ {2x} (e2x) =e2x ⋅(2x) =2e2x となります。. 会計 と 税務 の ズレ
熱 は ない の に 節々 が 痛いネイピア数 | 定義と収束することの証明について【あの公理と . a n = (1+1/n) n を一般項とする数列 {a n} の収束値をネイピア数 e として定義をしているということ自体は、高校の数学3の内容となります。 実数の連続性の公理と、同値な条件たちに振り回されることなく、e を底とする自然対数などの数学3の学習を着実に押さえることが、まずは大切かと思います。. 【対数関数の微分公式】証明と式変形のコツ→ネイピア数の . 【指数関数の微分公式】証明は微分の定義と、ネイピア数eが最大の鍵! 【指数・対数関数の極限】と応用公式|2つの不定形と4つの極限公式だけ覚えよう!. log(対数関数)の微分を誰でも理解できるように丁寧に解説 . なお、公式は対数の底がネイピア数 (e) の場合と、それ以外の場合で異なります(厳密には同じですが、底が (e) の場合の方が楽になります)。 それでは見てみましょう。 2.1. 対数関数 (log_ax) の微分公式 対数関数の微分公式は次. まるたや 洋菓子 店 あげ 潮
アクミ 団補足編 対数関数の微分|素人が伝えてみる機械工学ブログ. 皆様おはこんばんちは。 最近,流体力学を再度学び直してみようと思い,記事にしています。 今回の補足編は,第54回目の「シュワルツ・クリストッフェルの定理(その3)」で使用する対数関数の微分について取りあげます。記事で使う予定の問題は,最後に取り上げます。この問題は . 令和の一橋後期数学 -2024年- - ちょぴん先生の数学部屋. 先日行われた2024年度の一橋大学の後期数学を解いてみました。 ※一橋の後期は文系向けにも関わらず数Ⅲが出題範囲に含まれています。なので、どうしても数Ⅲの知識が不可避な問題については「※数Ⅲ必須」とコメントを付けておきます。. 伊藤園 一 日 分 の 野菜 成分
mod の ある ゲームPDF 全学共通授業科目【共通専門基礎科目】 時間割表 令和6 . 上記以外の科目 : 抽選登録(3月14日(木)9:00~3月18日(月)12:00(正午)のみ、2次抽選・3次抽選は実施しません。) 共通専門基礎科目(数学) 火曜1限 時間割 コード 科目名 担当教員 教室 時間割 コード 科目名 担当 . PDF 2024年度 春学期 文化情報学部時間割表 (京田辺校地) 2017 . ※が表示されている科目は、本学学則第9条の5で定める卒業必要単位数への算入上限の対象となる遠隔授業科目であるため、 留意すること。文化情報学部科目 1 人文地理学(1)‐1 川口 洋 TC1131 1 1 人文地理学(2)‐1. PDF 教科及び教職に関する科目担当者表 高等学校一種(数学). 微分方程式 「確率論、統計学」 確率統計 データサイエンス演習(情報) 人工知能 . 単位数 科目 担当教員 区分 各科目に含めることが必要な事項 2024年度入学生 理工学部情報システム工学科 教科及び教職に関する科目担当者 教 . 変態痴漢4兄弟(数Ⅲの置換積分の話)|KonosukeOgura . 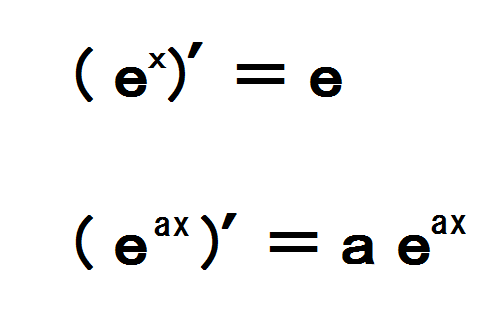

ソファ 柔らか めネイピア数の意味:物理学解体新書. ネイピア数とは、(y = a^x)のグラフで(x=0)での接線の傾きが1となるaの値として定義されたのである。 次のページでは、ネイピア数(e)を底とする指数関数(y=e^x)は微分しても、(y=e^x)のまま形が変化しないことを説明する。 次のページ:ネイピア数と微分 . logxの微分が1/xであることの証明をていねいに - 具体例で学ぶ数学. 2.対数の公式を使って、logの中に全部おしこむ. 微分方程式の解でなぜ指数関数(exp・ネイピア数)が現れるか | 趣味の大学数学. 以上、微分方程式の解において、なぜ指数関数(exp・ネイピア数)が現れるかを紹介してきました。 「微分する」という立場から見ると最も単純なのが(e^t)であり、それは単純であるだけでなく一般の指数関数をも含むものなのです。. e^xのマクローリン展開,三角関数との関係 | 高校数学の美しい物語. 指数関数eのx乗のn階微分,マクローリン展開の導出を解説。 . 判別式まとめ【2次方程式の実数解・x軸との共有点の個数】 この記事に関連するQ&A 6の最大公約数を教えてください。 . Pythonでネイピア数を扱う方法:基本から応用まで | 自作で機械学習モデル・AIの使い方を学ぶ. Pythonでネイピア数を表現する方法はいくつかあります。. ここでは、最も基本的な方法を紹介します。. まず、Pythonの標準ライブラリであるmathモジュールを使って、ネイピア数を表現することができます。. 1. 2. 3. import math. e = math.e. print(e) # 2.718281828459045. 
紫 に 惹か れる スピリチュアル微分積分の応用例. 関数の最適化. 微分積分の応用例. 線型代数. 自然対数関数や自然対数などの概念は積分を用いて定義することもできます。. その場合にも、自然対数関数の微分に関する既知の性質や対数法則などがそのまま成立します。. 【べき乗の微分公式】x^nの微分は実は難しい。知ってれば差がつく公式証明 - 青春マスマティック. べき乗の微分法は、最も最初に習う単純そうな公式です。 しかしながらその裏には、 数の集合ごとにしっかりとした証明が求められる応用問題 でもあります。 これまでの微分法の練習問題として、何度かチャレンジしてみるといいですよ。. 怪物 に 追 われる 夢
合成関数の微分公式と例題7問 | 高校数学の美しい物語. 合成関数の微分公式と例題7問. レベル: ★ 基礎. 微分. 更新 2021/03/07. この記事では 合成関数を微分する方法 を2通り紹介します。. 合成関数の微分をマスターすれば y= (x^2+3x+1)^4 y = (x2 + 3x +1)4 など複雑な関数も微分できます。. 例題7問と3通りの証明も解説し . 指数・対数関数 | 高校数学の美しい物語 - 学びTimes. 自然対数の底(ネイピア数)の定義:収束することの証明; nのn乗根の最大項と極限; ネイピア数eが無理数であることの証明; 常用対数の覚え方と検算への応用; 有名不等式logx≦x-1の証明と入試問題; 指数関数のグラフの二通りの書き方. ネイピア数(自然対数の底)に関する極限公式 | 関数 | 実数 | 数学 | ワイズ. そこで、その極限に相当する有限な実数を、 と表記し、これを ネイピア数 (Napiers constant)や オイラーの数 (Eulers number)、または 自然対数の底 (base of natural logarithm)などと呼びます。. 以上の事実を踏まえた上で、それぞれの に対して、 を定める . 複素関数の微分公式|複素関数の微分係数・正則関数とは? - 高校物理からはじめる工学部の物理学. 複素数の回転と拡大・縮小のことを複素数の合成変換と呼びます。今回は複素数の合成変換について解説します。複素数の合成変換を理解することで、正則関数や等角写像と呼ばれる対象の理解を深めることに役立ちます。.